ODAL

Overview

In a multicenter study, our ODAL algorithm allows researchers to fit a logistic regression model across multiple data sets, without the need of directly sharing subject-level information. The logistic regression model is a commonly used approach to model a binary outcome and a set of explanatory variables, which is a foundational method for studying associations, causal effects, and predicting risk of a certain event. Before conducting the multicenter analysis, all datasets have to be converted to a unified format where all the variables are defined in a standard way (e.g, OMOP Common Data Model). We require one of the sites to be the coordinating site, and the rest to be the participating sites. The coordinating site is responsible for obtaining and broadcasting the initial value of model parameters, synthesizing information obtained from other sites, and obtaining the final results. The participating sites only need to calculate the aggregated data and transfer them to the coordinating site. A more detailed description is provided below.

Logistic Regression Model

Suppose we have K sites, and the coordinating site is the first site. For the i-th individual in the j-th site, we denote the binary outcome to be \(y_{ij}\), and a vector of explanatory variables to be \(z_{ij}\). Let \(x_{ij} = (1, z_{ij}^{T})^T\) The logistic regression model assumes that

\(logit(Pr(y_{ij}=1)|x_{ij}) = x_{ij}^{T}\beta\)

where \(logit(t) = log\left \{ t/(1-t) \right \}\) and \(\beta\) is the vector of intercept and regression coefficients.

Algorithm

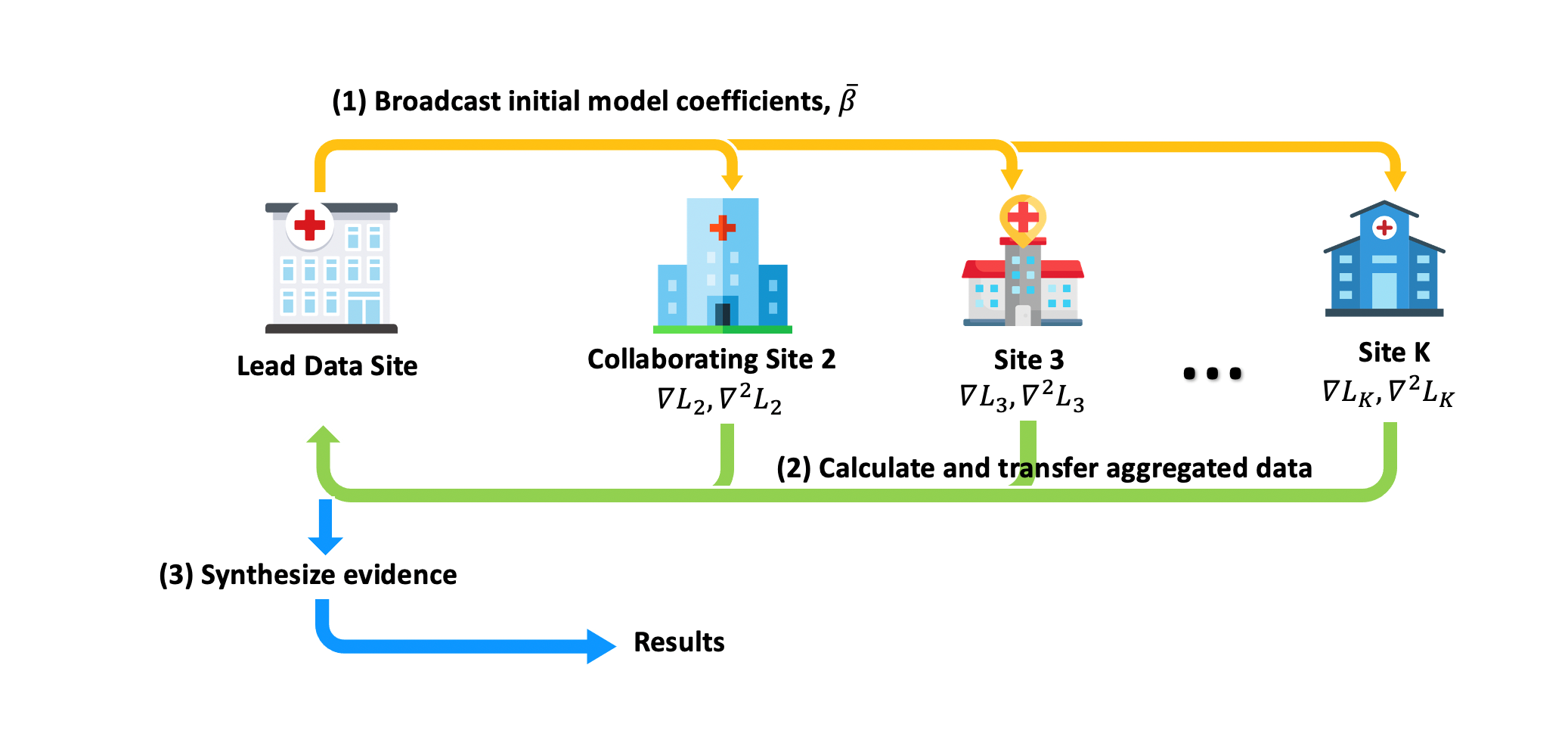
Figure 1: Schematic illustration of the ODAL algorithm

Our algorithm has three steps:

1. First, the coordinating site fits a logistic regression model using its own data, and share the estimates of regression coefficients \(\bar{\beta}\) to the participating sites.
2. Second, each participating site calculates the first, and the second order gradients of their own likelihood function, which are evaluated at the initial value \(\bar{\beta}\). Explicit form of calculating these two terms can be found in [1]. These aggregate data are then transferred to the coordinating site.
3. Third, the coordinating site uses the aggregate information and it own individual level data to obtain an improved estimate of \(\beta\).

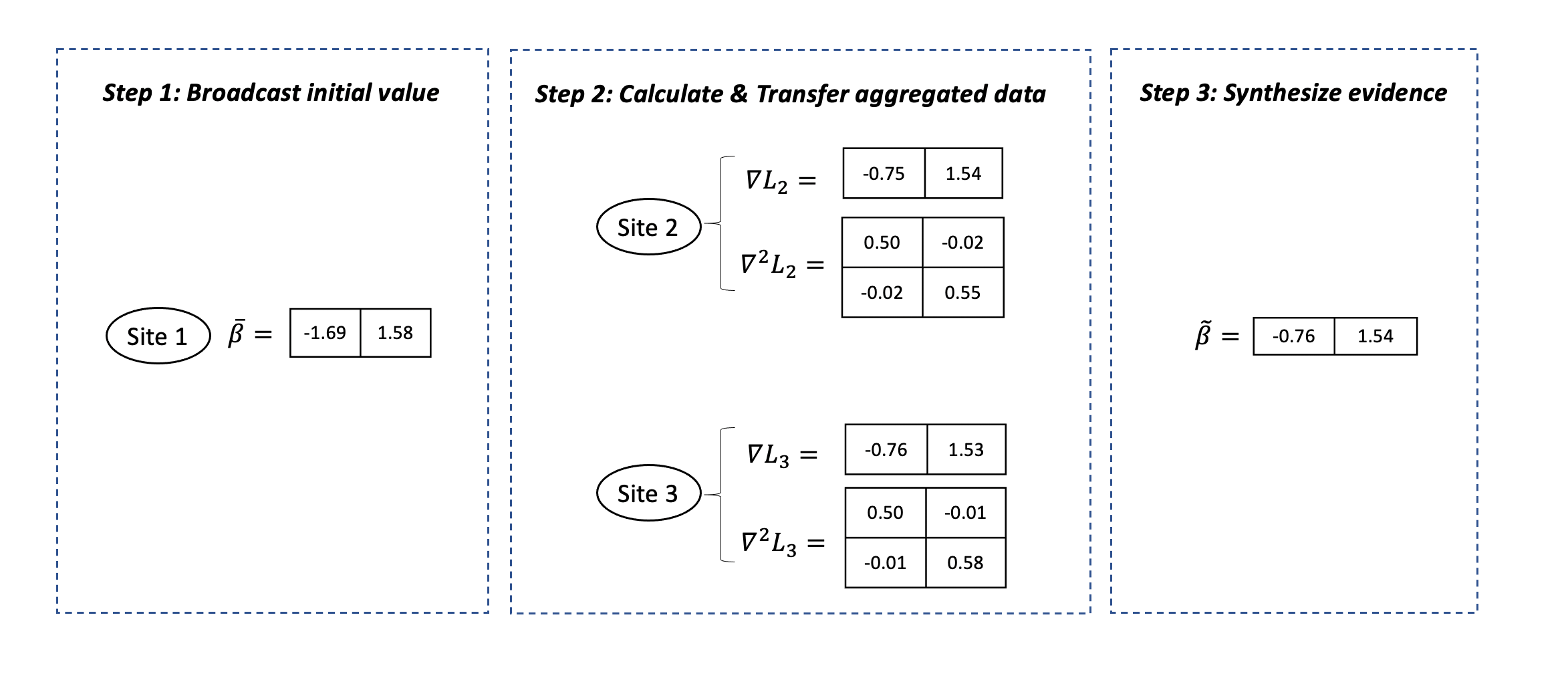
Figure 2 below give an example of the information shared in each step in a setting with one explanatory variable in the model. For p explanatory variables, each site need to transfer in total (p+1)+p* (p+1) numbers.

Sample code

 Set the “control” in R as beow to start ODAL algorithm

control <- list(project_name ='Lung cancer study',
                step = 'initialize',
                sites = c('site1', 'site2', 'site3'),
                heterogeneity = FALSE,
                model = 'ODAL',
                family = ' binomial',
                outcome = "status",
                variables = c('age', 'sex'),
                optim_maxit = 100,
                lead_site = 'site1',
                upload_date = as.character(Sys.time()) )
demo(ODAL)

Reference

[1] Duan, R., Boland, M., Liu, Z., Liu, Y., Chang, H., Xu., H, Chu, H., Schmid, C., Forrest, C., Holmes, J., Schuemie, M.J., Berlin, J.A., Moore, J.H. and Chen,Y., (2019). Learning from electronic health records across multiple sites: a computationally and statistically efficient distributed algorithm. Journal of the American Medical Informatics Association 27(3), pp.376-385.

[2] Duan, R., Chen, Z., Tong, J., Luo, C., Lyu, T., Tao, C., Maraganore, D., Bian, J. and Chen, Y., 2020. Leverage Real-world Longitudinal Data in Large Clinical Research Networks for Alzheimer’s Disease and Related Dementia (ADRD). medRxiv.