Overview
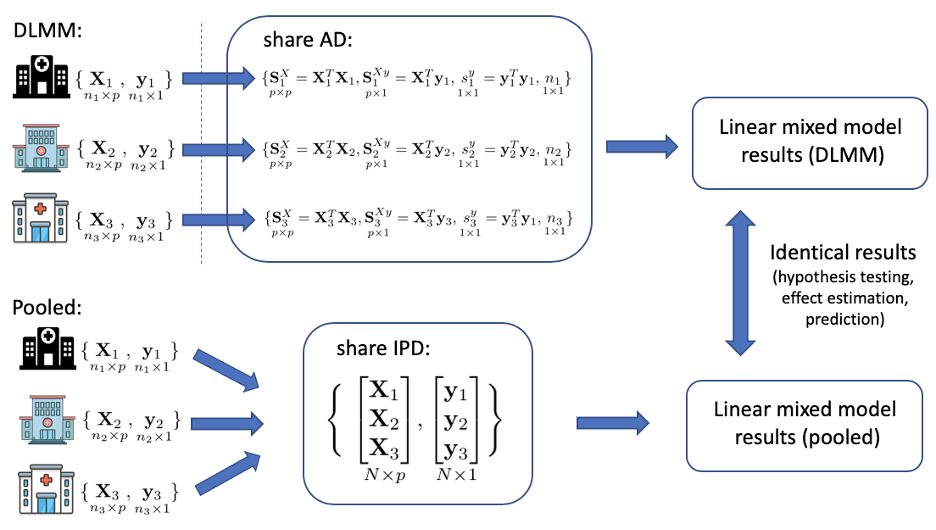
In a multicenter study, our DLMM algorithm allows researchers to fit a linear mixed model (LMM) across multiple data sets, without the need of directly sharing subject-level information. The LMM is an extension of the linear model and assumes site-specific random-effects besides the common fixed-effects of covariate variables on the continuous outcome. The estimation of the common fixed-effects enables general knowledge discovery, while the estimation of the random-effects allows site-specific prediction. Before conducting the multicenter analysis, all datasets have to be converted to a unified format where all the variables are defined in a standard way (e.g, OMOP Common Data Model). The DLMM algorithm requires each site to contribute some aggregated data (AD) only once, but achieves identical results as if all the individual patient data (IPD) are pooled together. Any site, even a site that does not hold any IPD data can be the coordinating site and collect the AD from the participating sites and fit the model. A more detailed description is provided below.
Linear Mixed Model
Suppose we have K sites, and the coordinating site is the first site. For the i-th individual in the j-th site, \(y_{ij}\) is the continuous outcome, \(x_{ij}\) is the p-dimensional covariate vector, \(\beta\) is the vector of fixed effects, \(z_{ij}\), the q-dimensional covariate vector having random effect \(u_{ij}\), and \(\epsilon_{ij}\) is the random error.
\(y_{ij} = x_{ij}^{T}\beta + z_{ij}u_{ij} + \epsilon_{ij}, i = 1, …, K, j = 1, …, n_{i}\)
where \(u_{i} \sim N(0, V), \epsilon_{ij} \sim N(0, \sigma^2)\). The random effects covariates \(z_{ij}\) is assumed to be part or all of \(ux{ij}\). The algorithm requires the i-th site to contribute some aggregated data, i.e. the p×p matrix \(S_{i}^{X} = X_{i}^{T}X_{i}\), the p×1 vector \(S_{i}^{Xy} = X_{i}^{T}y_{i}\), the scalar \(s_{i}^{y} = y_{i}^{T}y_{i}\) and the sample size \(n_i\) to fit the model.
Algorithm
Our algorithm has two steps:
- First, in site \(i =1, …, K\), calculate and send \(S_{i}^{X} = X_{i}^{T}X_{i}\), \(S_{i}^{Xy} = X_{i}^{T}y_{i}\), \(s_{i}^{y} = y_{i}^{T}y_{i}\), and sample size \(n_{i}\) to the coordinating site.
- Second, the coordinating site performs the model fitting, including testing for the random effects, estimating the variance components \(V\), fixed-effects \(\beta\) and random-effects \(u_i\) (i.e. BLUPs).
Reference
[1] Luo, C., Islam, M.N., Sheils, N., Reps, J., Buresh, J., Duan, R., Tong, J., Edmondson, M., Schumie, M.J., Chen, Y. (2020) Lossless distributed linear mixed model with application to integration of heterogeneous healthcare data. medRxiv2020.11.16.20230730; doi: https://doi.org/10.1101/2020.11.16.20230730